| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- Pull Request
- WSSS
- CellPin
- 기초확률론
- docker attach
- ssh
- docker exec
- cocre
- numpy
- airflow
- Decision Boundary
- 백신후원
- aiffel exploration
- vscode
- 오블완
- IVI
- cs231n
- docker
- 프로그래머스
- AIFFEL
- 코크리
- 도커
- GIT
- Jupyter notebook
- 사회조사분석사2급
- Multi-Resolution Networks for Semantic Segmentation in Whole Slide Images
- logistic regression
- 히비스서커스
- 티스토리챌린지
- HookNet
- Today
- Total
히비스서커스의 블로그
[CS231n 4] Introduction to Neural Networks 본문
※ 이 내용들은 전적으로 stanford university의 CS231n 2017 4강 강의 내용을 기반으로 작성하였음을 먼저 밝힙니다. ※
이전 3장에서는 Loss Function과 Opitmization을 살펴보았다.
2021/01/13 - [Programming/CS231n] - [Lecture 3] Loss Functions
[Lecture 3] Loss Functions
※ 이 내용들은 전적으로 stanford university의 CS231n 2017 3강 강의 내용을 기반으로 작성하였음을 먼저 밝힙니다. ※ 이전에 공부한 내용에서는 Linear classification의 모델의 구조를 살펴보았다. 20.
biology-statistics-programming.tistory.com
2021/01/18 - [Programming/CS231n] - [Lecture 3] Optimization
[Lecture 3] Optimization
※ 이 내용들은 전적으로 stanford university의 CS231n 2017 3강 강의 내용을 기반으로 작성하였음을 먼저 밝힙니다. ※ 2021/01/13 - [Programming/AIffel] - [Day 9] Loss Functions [Day 9] Loss Function..
biology-statistics-programming.tistory.com
이번 4장에서는 Backpropagation과 Neural Networks에 대해 알아보자

-Backpropagation
우리는 최적화 이론에서 최종 손실함수가 최소가 되도록 하는 가중치 행렬을 찾기 위해 gradient를 구하였다.
backpropagation은 gradient를 얻기위해 computational graph 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용한다.
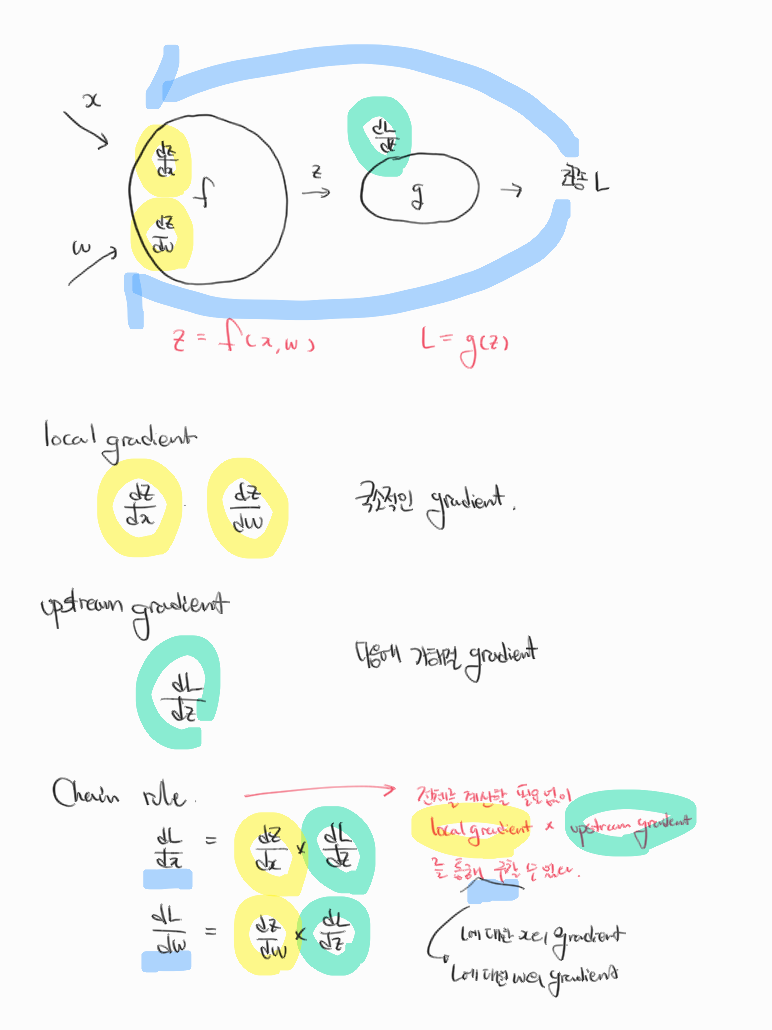
앞에는 주로 계산과정이 많아 이해한대로 정리해보았다.
계산은 아래를 보면 참조할 수 있다.

역전파 계산방법
1. 오른쪽에서부터 upstream gradient(빨간색 값)은 그대로 곱해준다.
2. 노드에 해당하는 함수를 미분해준다. 미분된 함수가 바로 local gradient이다.
3. local gradient 함수에 값(초록색)을 넣어주고 최종적으로 계산한다.
정확한 설명은 아니지만 흐름을 이해하는데 도움을 주고자 표현을 위와같이 해보았다.
하나의 스칼라 값을 가지고 계산을 할 경우는 생각보다 간단하지만, 벡터의 구조를 이루게 될 경우 자코비안 행렬을 고려해주어야 한다.

복잡하지만 위와 같은 절차라고 생각하면 된다.
여기서 발생하는 문제가 하나 있는데 원래의 순서대로 local gradient 와 upstream gradient를 곱해줄 경우 행렬이 성립되지 않는 경우가 생긴다. 이럴 경우 순서를 바꾸어 곱하여 행렬이 성립하도록 해주어야 한다. (개인적인 직관으로 행렬이 성립이 안되는 이유는 원래 곱해지던 순서가 달라졌기 때문이 아닐까라고 생각한다.)

forward : 순방향으로 식이 전개되어 나간다. 이때 각 노드마다 값을 저장해주어야 한다. (입력: x,y, 출력: z)
backward: 역방향으로 식이 전개되어 나간다. 이때 forward 에서 저장되었던 값들을 불러들어와 chain rule로 local gradient와 upstream gradient을 곱하여 계산한다. (입력: dz, 출력: dx, dy)
이제 Neural Networks를 알아보자.


우리가 이전까지 쓰던 분류기는 다양한 선형 score함수를 이용했다. 하지만 이제 층을 여러 겹으로 하여 비선형 문제도 해결할 수 있게 될 것이다. (여기서 max (0, Wx)함수는 비선형 함수이다!!)
신경망은 비선형의 복잡한 함수를 만들기 위해서 간단한 함수들을 계층적으로 여러 개 쌓아올린 집합이다.
이는 여러 단계의 계층적 계산이 이루어져 있는데 여기서 행렬 곱, 중간에 비선형 함수와 함께 선형 레이어를 여러개 쌓아 계산하는 것이다. 이를 통해 우리는 비선형 문제를 해결할 수 있다. (2장에서 말 머리가 2개를 구분하지 못했던 문제)

신경망은 뉴런과 비슷하여 붙여진 이름이다.
위의 그림을 보며 둘의 공통된 부분을 한 번 살펴보자.
위의 뉴런에서 신호 전달은 다음과 같다.
1. 외부의 자극을 수상돌기가 받아들인다.
2. 역치 이상의 자극일 경우 그 자극은 축삭돌기를 건너 축삭돌기 말단으로 전해진다.
3. 축삭돌기 말단에서 신호물질이 방출되면 다음 뉴런의 수상돌기가 받아들여 1~2의 과정이 반복된다. (최종적으로 기관에 도달)
Compytational node는 다음과 같다.
1. 입력 신호는 x(x0, x1, x2) 이다.
2. 이를 가중치가 받아들여 곱하고 활성화함수에 넣어준다. (이 값이 1과 유사하게 나올경우가 역치 이상의 자극과 비슷하다고 개인적으로 생각한다.)
3. 이 값이 최종적으로 나와 다른 입력신호로 들어가게 된다.
그렇다면 여기서 나온 활성화 함수란 무엇일까?
활성화 함수는 가중치와 입력값이 곱해지고 바이어스까지 더해진 값을 받아 그 값을 뱉어내는 함수인데 이 과정에서 비선형과정이 일어난다고 한다. 자세한 과정은 아래에서 확인하면 좋다.
colah.github.io/posts/2014-03-NN-Manifolds-Topology/
Neural Networks, Manifolds, and Topology -- colah's blog
Neural Networks, Manifolds, and Topology Posted on April 6, 2014 topology, neural networks, deep learning, manifold hypothesis Recently, there’s been a great deal of excitement and interest in deep neural networks because they’ve achi
colah.github.io
활성화 함수는 아래와 같다.

주로 relu 함수를 많이 쓴다고 한다. (다른 함수들 같은 경우 미분을 계속할 경우 기울기가 소실되기 때문이라고 한다.)

위와 같이 신경망을 부르는 방법은 두개이다.
왼쪽과 같이 input layer - hidden layer - output layer의 구성인 경우
2-layer Neural Net이나 1-hidden-layer Neural Net 이라고 부른다.
오른쪽과 같이 input layer - hidden layer1 - hidden layer2 - output layer의 구성인 경우
3-layer Neural Net이나 2-hidden-layer Neural Net 이라고 부른다.

네트워크 안의 각 노드에 forward pass를 수행하는 것은 뉴런의 행동과 같다. 각 히든 레이어는 완전한 벡터인 것이다.
행렬곱셈을 통해 뉴런 값을 계산하는 방식으로 쓰면 뉴런의 전체 레이어를 효율적으로 평가할 수 있다.
F: sigmoid 함수
x: 받은 데이터
h1: 가중치와 데이터의 내적(곱)에 바이어스를 더해줌(x*W1+b)
h2: 가중치와 전에 얻은 값(h1에서 나온 값을 활성화 함수에 넣어 얻은 비선형 형태의 값)에 바이어스를 더한 값
out: 최종 값
다음 시간에는 CNN 에 대해 자세히 알아보자!
2021.01.25
히비스서커스
'Theory > Computer Vision' 카테고리의 다른 글
| [CS231n 6] Training Neural Networks 1 (0) | 2021.02.07 |
|---|---|
| [CS231n 5] Convolutional Neural Networks (0) | 2021.02.01 |
| [CS231n 3] Optimization (0) | 2021.01.18 |
| [CS231n 3] Loss Functions (0) | 2021.01.13 |
| [CS231n 2] Image Classification (4) | 2020.12.30 |




