| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- docker exec
- 사회조사분석사2급
- ssh
- Jupyter notebook
- 백신후원
- aiffel exploration
- WSSS
- 오블완
- IVI
- 코크리
- HookNet
- airflow
- docker
- docker attach
- 히비스서커스
- Pull Request
- Multi-Resolution Networks for Semantic Segmentation in Whole Slide Images
- 기초확률론
- GIT
- CellPin
- 티스토리챌린지
- vscode
- Decision Boundary
- numpy
- cs231n
- 프로그래머스
- 도커
- logistic regression
- cocre
- AIFFEL
- Today
- Total
히비스서커스의 블로그
[CS231n 5] Convolutional Neural Networks 본문
※ 이 내용들은 전적으로stanford university의 CS231n 2017 5강 강의 내용을 기반으로 작성하였음을 먼저 밝힙니다.※
이전 4장에서는 Backpropagation과 Neural Networks에 관하여배웠다.
2021/01/25 - [Programming/CS231n] - [lecture 4] Introduction to Neural Networks
[lecture 4] Introduction to Neural Networks
※ 이 내용들은 전적으로 stanford university의 CS231n 2017 4강 강의 내용을 기반으로 작성하였음을 먼저 밝힙니다. ※ 이전 3장에서는 Loss Function과 Opitmization을 살펴보았다. 2021/01/13 - [Progra..
biology-statistics-programming.tistory.com
이번 5장에서는 Convolution Neural Networks에 대해 알아보자

Fully Connected Layer 모델의 연산
Fully Connected Layer에서는 다음과 같이 연산을 하였다.

입력으로 32 x 32 x 3 의 이미지가 들어오게 되면 길게 펴서 3072차원의 벡터로 만든 후 가중치 W(이 예시에서는 W가 10x3072 행렬)를 곱하였다. 얻어진 내적의 값들이 10개의 행으로 activation 을 이루게 된다.
Convolution Layer의 연산
Convolution Layer는 길게 펴는 FC Layer와의 방식과는 다르게 기존의 구조를 보존시킨다.
작은 필터가 이미지를 슬라이딩하면서 공간적으로 내적을 수행한다.

필터는 입력의 깊이만큼 확장된다. image(32X32X3)에서 3의 깊이를 가지므로 filter(5X5X3)에서 3의 깊이를 가지게 된다.
여기에서 5X5X3 이란 의미는 저만큼의 연산을 해준다는 것이고 그 후에 bias term을 더해주게 된다. 기본적으로 W(transpose)x + b를 연산하는 것이다.
학생질문: 내적을 할때는 긴 벡터를 사용하는 것이냐?
각 원소끼리 Convolution하는 것이나 FC layer에서 쭉 편 다음에 곱하는 것이나 같다고 볼 수 있다.
학생질문: 가중치에 transpose를 하는 이유는?
어떻게 표현하느냐의 차이지 직관이 있는 것이 아니다.
서로 다른 필터로 인한 서로 다른 activation map의 생성
보통 convolution layer에서는 필터 마다 다른 특징을 추출해야 하기에 여러 개의 필터(필터에 들어있는 원소의 값이 다르다는 의미)를 사용한다.

즉, 위에 보이는 파란색 activation map 과 초록색 actviation map이 다른 것이다. (필터의 원소의 값이 다르므로 그 내적한 값도 달라질 것이기 때문)

만약 5 x 5 필터가 6개가 있다면 28 x 28 activation map 6개를 얻게 될 것이다.

여러 개의 layer를 통한 계층적 학습
이 activation map 사이에 activation function들 예를 들면 Relu와 같은 것들을 사용할 수 있고, 가끔 pooling layer도 들어갈 것이다. 여기서 각 layer의 출력은 다음 layer의 입력이 될 것이다. 여러 개의 layer들을 쌓고나면 결국 필터들이 계층적으로 학습하는 것을 볼 수 있게 된다.

Low-level feature에서는 Edge와 같은 것들을 얻어낸다. 다음으로 Mid-level feature에서는 코너와 blob과 같은 것들을 그리고 high-level feature를 보면 더 넓은 객체와 닮은 것들을 볼 수 있는 것이다.
기본적으로는 필터를 가지고 이미지에 슬라이딩하면서 모든 위치에서 내적을 수행하게 된다.

각각의 32개의 5X5 필터가 만들어낸 activation의 모양은 filter의 원소가 다르기 때문에 각기 다를 것이다.
Stride
그렇다면 필터가 슬라이딩을 한다는 것이 무슨 뜻일까?
FxF 필터가 NxN 이미지를 슬라이딩을 한다고 해보자. 한 번에 몇 칸을 움직일 것인지를 나타내는 것이 stride이다.
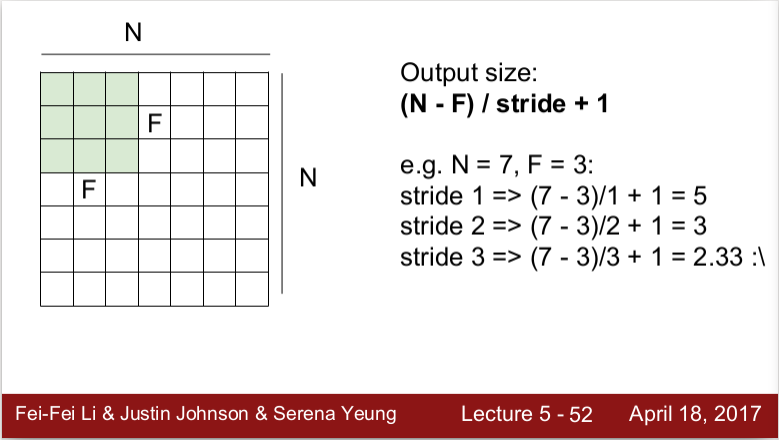
stride에 따라서 output의 크기가 달라지는데 그 공식은 위와 같다.
pad
그런데 생각해보면 모서리에 있는 부분은 중앙에 있는 부분들보다 더 적게 정보가 입력되게 된다. 이러한 점을 고려해준 것이 바로 padding이다. 모서리 부분에 다른 값들을 추가하는 것인데 보통 0을 넣는 zero-pad를 많이 사용한다.

그렇다면 padding을 처리해주었을 때 필터를 걸쳐 나온 activation map의 크기는 어떻게 될까?
stride 를 고려할 때의 공식은 (N-F)/stride + 1이었다. 여기서 padding을 1로 해주면 N에 2를 더해주어야 한다.
따라서, 정리해보자면 (N+2*padding-F)/stirde + 1이라고 할 수 있다.
padding을 처리해주지 않는다면 이미지의 크기는 필터를 거치면서 계속 줄어들게 되고 공간적인 정보도 줄어들 것이다.

layer에 필요한 파라미터의 개수
그렇다면 layer에 필요한 파라미터의 개수를 생각해보자. 파라미터란 모델 내부에서 결정되는 변수이다.

32x32x3의 이미지에 5x5 filter 10개를 stride = 1, pad = 2로 적용한다고 하면 파라미터의 숫자는
(5x5x3(필터 내부 원소의 개수) + 1 (바이어스의 크기)) x 10(필터의 개수) = 760이 된다.

1 x 1 Convolution layer
1 x 1 Convolution layer는 입력의 전체 Depth에 대한 내적을 수행하는 것이다. 1 x 1 Convolution layer을 통해서는 공간적인 정보는 변하지 않는다. 그러나 이를 통해 주로 output size 를 줄여주는역할 즉, 파라미터의 크기를 줄여주는 역할을 한다.
학생질문: stride를 선택하는데 가질 수 있는 직관이 있는가?
크게 가져갈수록 출력은 점점 작아진다. 이미지를 다운 샘플링하는 것은 풀링하는 것과 비슷하지만 이보다 더 좋은 성능을 보이기도 한다.
activation map의 사이즈를 줄이면 나중에 Convolution layer의 출력이 작아지게 된다. Convolution layer의 출력은 FC layer와 연결되어 있으므로 나중에 FC layer에서 필요한 하이퍼 파리미터의 수가 줄어들 것이다.
Convolution layer와 Fully Connected layer의 차이점 비교
Convolution layer의 경우

각 필터를 통해서 같은 지역에서 추출된 서로 다른 특징이다. (각 필터를 구성하는 벡터 값과 바이어스가 다르기 때문이다.)
또한, 필터를 통해서 이미지의 부분부분의 특징들을 추출하기 때문에 공간적인 정보를 담을 수 있다.
Fully Connected layer의 경우

이미지의 shape 을 쭉 펴서 전체를 연결한 후 사용한다. 따라서, 모든 정보를 담지만 공간적인 정보를 담을 수 없게 된다.
Pooling layer

하는 일: Down sampling.
Depth에는 영향을 주지 않으며 각 activation map을 공간적으로 줄여준다.
주로 쓰는 방법은 max polling으로 필터 안에서 가장 큰 값을 추출하는 방법이다.
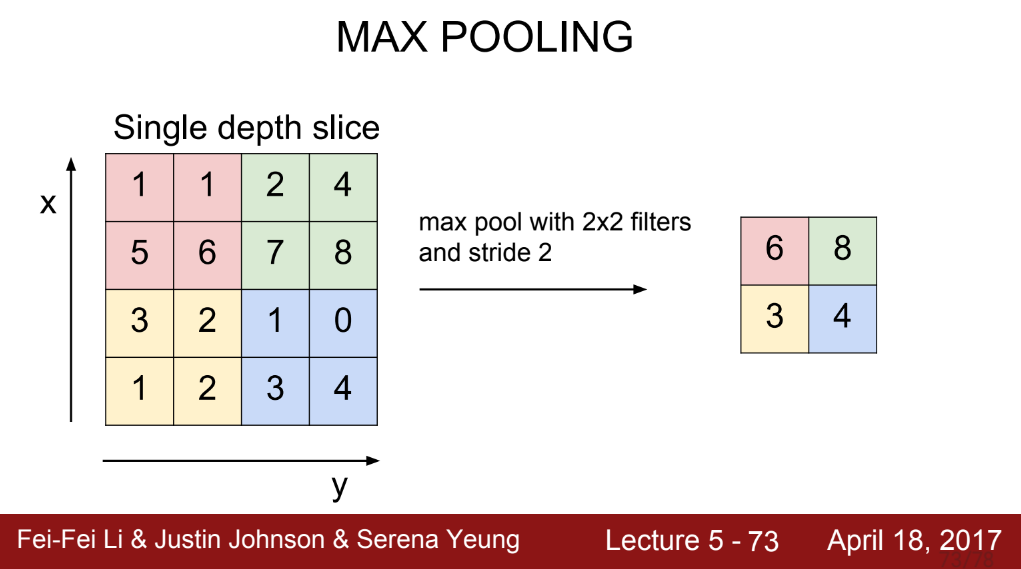
그렇다면 왜 필터들의 값의 정보를 잘 담을 수 있는 평균이 아니라 max값을 넣어주는 것일까?
필터에서 추출된 값은 이 필터가 각 위치에서 얼마나 활성되었는지를 나타내는 값들이다.
따라서, max pooling은 그 지역이 어디든지 입력받은 신호(값)에 대해 그 필터가 얼마나 활성화 되었는지를 알려준다.
즉, 필터의 값이 어디에 있었냐는 것보다는 그 값이 얼마나 큰지가 더 중요한 것이다.
풀링할 때 주로 쓰는 것은 2x2 filter를 쓰며 stride는 2를 사용한다.

Convolution layer -> ReLU -> Pooling layer의 과정
마지막 Convolution layer의 출력은 3차원 volume으로 이루어진다.
보통은 이 값들을 전부 펴서 1차원 벡터로 만들어주는 FC layer가 존재한다.
이를 통해 Convolution net의 모든 출력을 연결하게 된다. 마지막에는 공간적 구조를 신경쓰지 않아도 되기 때문이다.
이렇게 전부 다 하나로 통합시키고 최종적인 추론을 하면 Score가 출력으로 나오는 것이다.

처음에 Convolution layer를 거치면 activation map이 나온다. 이는 다시 ReLU함수를 거쳐 출력 값이 나오고 Pooling layer는 출력을 입력 받아서 Down sampling해주는 것이다.
전체 과정 요약
첫번째 Convolution layer를 거쳤을 경우 최하위 계층으로 edges와 같은 단순한 구조를 찾아낸다.
따라서, 각 자라에서 edge같은 것들이 얼마나 존재하는지를 의미한다.
두번째 Convolution layer를 거쳤을 경우 corner와 같은 좀 더 복잡한 구조를 찾아낸다.
따라서, 각 자리에 이와 같은 것들이 얼마나 있는지 보여주게 된다.
하지만 여기서 각 convolution layer의 입력이 원본 이미지가 아니라 이전 레이어에서 나온 edge maps와 같은 것이다.
이런 edge map 을 가지고 더 복잡한 것들을 추론할 수 있게 된다.
마지막 pooling layer를 거치기 전까지 각 값들은 각 필터가 가진 template를 얼마나 활성되었는지를 표현한다.
그리고 pooling layer를 거쳐 Down sampling 되고 FC layer를 거치면 이 정보들이 모여서 클래스 스코어를 최종적으로 만들어낸다.
2021.02.01.월
-히비스서커스-
'Theory > Computer Vision' 카테고리의 다른 글
| [CS231n 7] training neural network 2 (0) | 2021.02.14 |
|---|---|
| [CS231n 6] Training Neural Networks 1 (0) | 2021.02.07 |
| [CS231n 4] Introduction to Neural Networks (0) | 2021.01.25 |
| [CS231n 3] Optimization (0) | 2021.01.18 |
| [CS231n 3] Loss Functions (0) | 2021.01.13 |




