| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 백신후원
- AIFFEL
- aiffel exploration
- Decision Boundary
- 기초확률론
- airflow
- WSSS
- IVI
- docker attach
- 히비스서커스
- Pull Request
- vscode
- 코크리
- docker exec
- 도커
- Multi-Resolution Networks for Semantic Segmentation in Whole Slide Images
- logistic regression
- HookNet
- 오블완
- ssh
- Jupyter notebook
- GIT
- cs231n
- 티스토리챌린지
- 프로그래머스
- docker
- cocre
- 사회조사분석사2급
- numpy
- CellPin
- Today
- Total
히비스서커스의 블로그
[CS231n Midterm] Short Answer 본문
※이 내용들은 전적으로 stanford university의 CS231n 2017 Midterm문제와 Solution을 참조하여 작성하였음을 먼저 밝힙니다. 도움을 주신 아이펠 대전 1기 CS231n 풀잎스쿨 분들께 감사를 표합니다.※
1~2번 문제는 다음의 블로그를 참조해주세요!
https://shinest-programming.tistory.com/24
[cs231n]midterm 중간고사 풀이
2021.3.29 16:19 안녕하세요 프로그램밍을 배우는 빛나는 샤트입니다. 스탠포드 대학의 딥러닝 강의인 cs231n의 중간고사 풀이입니다. 문제와 풀이 pdf파일은 이 블로그 글의 하단의 github 링크에 있습
shinest-programming.tistory.com
3.1 Backpropagation
각 회로도의 forward pass activations 아래에 누락된 그라디언트를 채워라.
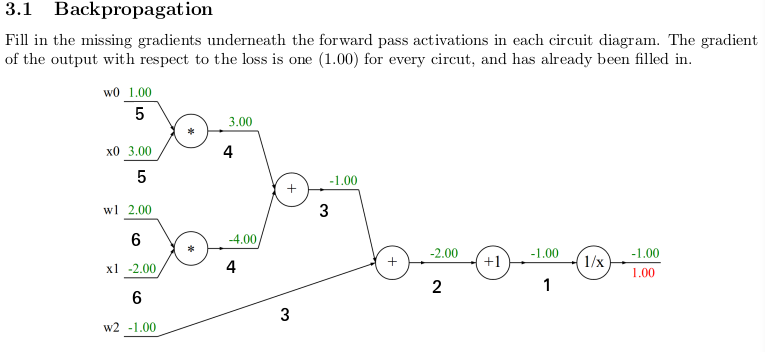
각 연산에 대한 편미분을 구해보자.
$ z = \frac{1}{x}$, $\frac{dz}{dx} = -\frac{1}{x^2} $
$ z = x+1$, $ \frac{dz}{dx} = 1 $
$ z = x + y$, $ \frac{dz}{dx}=1, \frac{dz}{dy}=1 $
$ z = x*y$, $ \frac{dz}{dx}=y, \frac{dz}{dy}=x $
이제 역순으로 보면서 gradient 값들을 구해보자.
- $\frac{1}{x}$의 미분함수 $-\frac{1}{x^2}$에 노드 계산의 최종 값인 -1 을 대입하고 upstream gradient인 1을 곱해주자.
$$ -\frac{1}{(-1)^2} * 1 = -1 $$ - $+1$의 $+$ 노드 연산의 미분함수 $1$에 upstream gradient인 1을 곱해주자.
$$ 1 * -1 = -1 $$ - $(w_{0}*x_{0} + w_{1}*x_{1}) + w_{2}$의 $+$의 미분함수 $\binom{1}{1}$에 upstream gradient인 -1을 곱해주자.
$$ \binom{1}{1} * -1 = \binom{-1}{-1} $$ - $w_{0}*x_{0} + w_{1}*x_{1}$의 $+$의 미분함수 $\binom{1}{1}$에 upstream gradient인 -1을 곱해주자.
$$ \binom{1}{1} * -1 = \binom{-1}{-1} $$ - $w_{0}*x_{0}$의 $*$의 미분함수인 각 변수에 대해 다른 변수$\binom{x_{0}}{w_{0}}$에 upstream gradient인 -1을 곱해주자.
$$ \binom{3}{1} * -1 = \binom{-3}{-1} $$ - $w_{1}*x_{1}$의 $*$의 미분함수인 각 변수에 대해 다른 변수$\binom{x_{1}}{w_{1}}$에 upstream gradient인 -1을 곱해주자.
$$ \binom{-2}{2} * -1 = \binom{2}{-2} $$
3.2 Convolutional Architectures
아래에 해당하는 레이어의 메모리 양과 파라미터 수를 구하여라.

아래의 표현들을 해석해보면
- Conv5-N이란 5X5필터로 padding이 2, stride가 1, channel이 N만큼 하여 이동한다는 뜻이다.
- Pool2란 2X2 max-pooling layer를 stride가 2가 만큼하여 출력한다는 뜻이다.
- FC-N이란 Fully-connected layer의 neurons이 N개라는 의미이다.
이를 근거하여 풀어나가보면
첫번째 CONV5-10의 메모리는 가로 x 세로 x channel인데
이때의 가로와 세로는{ 32 - (filter의 가로 or 세로) + 2*(Padding) }/ (Stride) + 1 에서 (32 - 5 + 2*2) / 1 + 1 = 32 이고 channel은 10 이므로, 32x32x10이 된다.
첫번째 CONV5-10의 파라미터 수는 channel x (filter의 가로 x filter의 세로 x depth + bias)이므로 10x(5x5x1 + 1)이 된다.
두번째 POOL2의 메모리는 가로 x 세로 x depth인데
이때의 가로와 세로는 (입력의 가로 or 세로 - filter의 가로 or 세로) / (Stride) + 1에서 (32 - 2) / 2 + 1 = 16이고 channel은 10 이므로, 16x16x10이 된다.
두번째 POOL2의 파라미터 수는 0이다. (Pooling layer의 파라미터 수는 항상 0이다.)
세번째 CONV5-10의 메모리도 첫번째와 마찬가지로 가로 x 세로 x channel인데
이때의 가로와 세로는 (16 - 5 + 2*2) / 1 + 1 = 16 이고 channel은 10 이므로, 16x16x10이 된다.
세번째 CONV5-10의 파라미터 수도 번째와 마찬가지로 channel x (filter의 가로 x filter의 세로 x depth + bias)이므로 10x(5x5x10 + 1)이 된다.
네번째 POOL2의 메모리도 두번째와 마찬가지로 가로 x 세로 x depth인데
이때의 가로와 세로는 (16 - 2) / 1 + 1 = 8이고 channel은 10 이므로, 8x8x10이 된다.
네번째 POOL2의 파라미터 수는 0이다.
마지막 FC-10의 메모리는 Fully connected layer에서의 volume으로 쭉 펼친 것이므로 channel x 1인데
channel은 10 이므로, 10x1이 된다.
마지막 FC-10의 파리미터 수는 channel x (입력의 가로 x 입력의 세로 x depth + bias)인데
이때의 channel은 10이고, 입력의 가로와 세로는 8, depth는 10, bias는 1개이므로
10x(8x8x10 + 1)이 된다.
3.3 Simple ConvNet
모든 변수가 scalar 값을 가지는 1-dimensional ConvNet을 고려하여 아래의 문제를 풀어라.

(a) 이 네트워크에서 파라미터인 것을 적어라.

맨 아래 입력 x들과 출력 z들의 관계식을 보면 k들이 x의 가중치가 되고, b는 bias가 되므로 $k_{1}, k_{2}, k_{3}$과 b는 파라미터가 된다.
다음으로 입력 z들은 max함수를 거쳐 출력 v들로 나오게 되는데 이는 파라미터와는 무관하다.
마지막으로 입력 v와 출력 y의 관계식을 보면 w들이 v의 가중치가 되고, a는 bias가 되므로 $v_{1}, v_{2}$와 a는 파라미터가 된다.
따라서, $k_{1}, k_{2}, k_{3}, b, v_{1}, v_{2}, a$가 이 네트워크의 파라미터가 된다.
(b) 아래의 답을 결정해라.

먼저 $L$과 $\hat{y}$의 관계식을 전개해보면 $L = \frac{1}{2}(y - \hat{y})^2 = \frac{1}{2}y - y \hat{y} + \frac{1}{2} \hat{y}^2$이 된다. 여기서 $y$에 대해 편미분을 진행해주면 $ \frac{\partial L}{\partial \hat{y}} = -y + \hat{y}$이 된다.
다음으로 $\hat{y}$ 와 $w_{1}, w_{2}, a$와의 관계식 $\hat{y} = w_{1} v_{1} + w_{2} v_{2} + a$에서 $w_{1}, w_{2}, a$에 대해 편미분을 진행해주면 $\frac{\partial \hat{y}}{\partial w_{1}} = v_{1}, \frac{\partial \hat{y}}{\partial w_{2}} = v_{2}$이다.
위 문제의 3가지 편미분은 local gradient x upstream gradient의 꼴로 나타낼 수 있으므로
$\frac{\partial L}{\partial w_{1}} = \frac{\partial L}{\partial \hat{y}} * \frac{\partial \hat{y}}{\partial w_{1}} = (-y + \hat{y}) * v_{1}$
$\frac{\partial L}{\partial w_{2}} = \frac{\partial L}{\partial \hat{y}} * \frac{\partial \hat{y}}{\partial w_{2}} = (-y + \hat{y}) * v_{2}$
$\frac{\partial L}{\partial a} = \frac{\partial L}{\partial \hat{y}} * \frac{\partial \hat{y}}{\partial a} = (-y + \hat{y}) * 1$
이 된다.
(c) loss L에 대한 두번째 레이어의 v들의 gradient가 주어졌을 때 첫번째 레이어의 z들에 관한 아래의 gradient식을 결정하여라.

여기서 가장 난감해할 수 있는 부분이 max함수에 대한 gradient를 구하는 것이다.
먼저, $z_{1}$에 대해 미분하는 것만을 고려해주는 것이므로 $max(z_{1}, z_{2}, 0)$에서 $z_{1}$이 없는 경우는 0이 되므로 $z_{1}$이 남아있는 경우에 대해서만 고려해주면 된다. 따라서, max함수를 $max(z_{1}, z_{2}, 0) = max(z_{1}, z_{2})*max(z_{1}, 0)$ 같이 변형할 수 있다.
그 다음으로 $max(z_{1}, z_{2})$와 $max(z_{1}, 0)$에 대한 편미분을 구하는 것에서는 indicator function에 대해서 알고 갈 필요가 있다. indicator function를 정말 간단하게 설명하면 특정 범위만 1로 보내고 나머지는 0으로 보내는 함수라고 할 수 있다.
$max(z_{1}, 0)$에서 $z_{1}$이 0보다 큰 경우에는 $z_{1}$이 나오게 되는데 이를 $z_{1}$로 미분할 경우 1이 된다. 0보다 작을 경우에는 0이 나오게 되는데 이를 $z_{1}$로 미분할 경우 0이 된다. 따라서, 이를 indicator function으로 나타낸다면 $\displaystyle I_{z_{1} \geq 0}$가 된다. 마찬가지로 $max(z_{1}, z_{2})$를 $z_{1}$로 미분하게 되면 $\displaystyle I_{z_{1} \geq z_{2}}$가 나오게 된다.
이제 위 문제의 편미분 식을 local gradient x upstream gradient의 꼴로 나타내보면
$\frac{\partial L}{\partial z_{1}} = \frac{\partial L}{\partial v_{1}} * \frac{\partial v_{1}}{\partial z_{1}} = \delta_{1}\displaystyle I_{z_{1} \geq 0}\displaystyle I_{z_{1} \geq z_{2}} $
$\frac{\partial L}{\partial z_{2}} = \frac{\partial L}{\partial v_{1}} * \frac{\partial v_{1}}{\partial z_{2}} + \frac{\partial L}{\partial v_{2}} * \frac{\partial v_{2}}{\partial z_{2}} = \delta_{1}\displaystyle I_{z_{2} \geq 0}\displaystyle I_{z_{2} \geq z_{1}} + \delta_{2}\displaystyle I_{z_{2} \geq 0}\displaystyle I_{z_{2} \geq z_{3}}$
$\frac{\partial L}{\partial z_{3}} = \frac{\partial L}{\partial v_{2}} * \frac{\partial v_{2}}{\partial z_{3}} = \delta_{3}\displaystyle I_{z_{3} \geq 0}\displaystyle I_{z_{3} \geq z_{2}} $
이 된다.
(d) loss L에 대한 첫번째 레이어의 z들의 gradient가 주어졌을 때 convolution layer filter의 k들에 관한 아래의 gradient 식을 결정하여라.

먼저 k들과 z들의 관계식을 적어보자.
$z_{1} = k_{1} x_{1} + k_{2} x_{2} + k_{3} x_{3} + b$
$z_{2} = k_{1} x_{2} + k_{2} x_{3} + k_{3} x_{4} + b$
$z_{3} = k_{1} x_{3} + k_{2} x_{4} + k_{3} x_{5} + b$
이 문제에서의 핵심은 $k_{1}, k_{2}, k_{3}$ 각각이 $z_{1}, z_{2}, z_{3}$ 모두와 연관되어 있어서 $k_{1}, k_{2}, k_{3}$ 각각에 대한 gradient를 구해주려면 $z_{1}, z_{2}, z_{3}$에 대한 gradient를 더해주어야 한다는 것이다.
이를 적용하여 위의 세 편미분 식을 local gradient x upstream gradient 로 나타내어 주면
$\frac{\partial L}{\partial k_{1}} = \frac{\partial L}{\partial z_{1}} * \frac{\partial z_{1}}{\partial k_{1}} + \frac{\partial L}{\partial z_{2}} * \frac{\partial z_{2}}{\partial k_{1}} + \frac{\partial L}{\partial z_{3}} * \frac{\partial z_{3}}{\partial k_{1}} = \delta_{1} * x_{1} + \delta_{2} * x_{2} + \delta_{3} * x_{3}$
$\frac{\partial L}{\partial k_{2}} = \frac{\partial L}{\partial z_{1}} * \frac{\partial z_{1}}{\partial k_{2}} + \frac{\partial L}{\partial z_{2}} * \frac{\partial z_{2}}{\partial k_{2}} + \frac{\partial L}{\partial z_{3}} * \frac{\partial z_{3}}{\partial k_{2}} = \delta_{1} * x_{2} + \delta_{2} * x_{3} + \delta_{3} * x_{4}$
$\frac{\partial L}{\partial k_{3}} = \frac{\partial L}{\partial z_{1}} * \frac{\partial z_{1}}{\partial k_{3}} + \frac{\partial L}{\partial z_{2}} * \frac{\partial z_{2}}{\partial k_{3}} + \frac{\partial L}{\partial z_{3}} * \frac{\partial z_{3}}{\partial k_{3}} = \delta_{1} * x_{3} + \delta_{2} * x_{4} + \delta_{3} * x_{5}$
이 된다.
(e) 일반적인 1D convolution layer에 대해 loss L에 대한 z의 gradient 값을 아래와 같이 알고 있을 때 convolution layer filter의 일반적인 k와 bias인 b에 대해 아래의 식을 결정하여라.

$z_{j}$에 대한 k와x, b에 대한 일반적인 관계식을 적용해보면 다음과 같다.
$z_{i} = k_{1} x_{i} + k_{2} x_{i+1} + ... + k_{m} x_{m+i-1} + b = \sum_{j=1}^{m} x_{i+j-1} k_{j} + b$
여기서 $z_{i}$를 $k_{j}$에 대해서 미분해주면 $\frac{\partial z_{i}}{\partial k_{j}} = x_{i+j-1}$이 된다. 또한, $z_{i}$를 $b$에 대해서 미분해주면 1이 된다.
$k_{j}$는 m개의 z들과 연관되어 있으므로 m개의 z들에 대한 gradient를 모두 더해주어야 한다. 이를 적용하여 위의 두 편미분 식을 local gradient x upstream gradient로 나타내주면
$\frac{\partial L}{\partial k_{j}} = \sum_{i=1}^{m} \frac{\partial L}{\partial z_{i}} * \frac{\partial z_{i}}{\partial k_{j}} = \sum_{i=1}^{m} \delta_{i} x_{i+j-1}$
$\frac{\partial L}{\partial b} = \sum_{i=1}^{m} \frac{\partial L}{\partial z_{i}} * \frac{\partial z_{i}}{\partial b} = \sum_{i=1}^{m} \delta_{i} $
이 된다.
-히비스서커스-
21.05.27 오타수정 (3-2. stride 1->2)
21.10.26 오타수정 (3-2. 10x(5x5x1 + 1) -> 10x(5x5x10 + 1)) (3-3-e. $x_{i+j+1}$ -> $x_{i+j-1}$)
22.01.26 오타수정 (3-3-d. z1 -> z1, z2, z3)
오타 지적해주신 분들께 감사드립니다.
'Theory > Computer Vision' 카테고리의 다른 글
| [CS231n 12] Visualizing and Understanding (0) | 2021.09.11 |
|---|---|
| [CS231n 11] Detection and Segmentation (0) | 2021.09.06 |
| [CS231n 9] CNN Architectures (2) | 2021.02.21 |
| [CS231n 7] training neural network 2 (0) | 2021.02.14 |
| [CS231n 6] Training Neural Networks 1 (0) | 2021.02.07 |




