[기초확률론 4] 조건부확률, 곱셈법칙, 베이즈 정리

기초확률론 네번째 포스팅으로 조건부확률, 곱셈법칙, 베이즈 정리에 대해 알아보겠습니다.

 

 

저번 시간에는 확률측도의 성질, 균등확률결과를 갖는 표본공간에 대해 알아보았습니다.

2021/01/22 - [Statistics/Probability_Theory] - [기초확률론 3] 확률측도의 성질, 균등확률결과를 갖는 표본공간

[기초확률론 3] 확률측도의 성질, 균등확률결과를 갖는 표본공간

 

 

확률측도의 성질은 우리가 직관적으로 생각할 수 있는 것들과 같은 성질을 가지고 있었습니다. 또한, 이러한 확률측도로 표본공간의 각 원소들의 확률이 모두 동일할 때 균등확률결과를 갖는다고 하고 이러한 표본공간을 균등확률결과를 갖는 표본공간이라고 하였습니다.

 

앞에서 살펴본 확률들은 표본공간 안에서 하나의 사건에 대해서만 측정하였고 두 사건이 동시에 일어나는 사건에 관한 Union과 Intersection에 대해서만 알아보았습니다. (예를 들자면 공정한 주사위 2개를 동시에 던져서 나오는 눈의 합이 8인 경우의 확률을 구하는 경우라고 하겠습니다.) 그런데 만약에 사건들이 동시에 일어나지 않는 경우에는 어떻게 해야 할까요?? 이런 경우 먼저 일어난 사건의 확률이 다음에 일어날 사건의 확률에 영향을 줍니다.

 

 

조건부 확률

 

조건부 확률의 정의는 다음과 같습니다.

 

 S가 하나의 표본공간이고, $E_{1} \subset S$, $E_{2} \subset S$ 일 때 (단, $E_{1}$, $E_{2}$ 이 표본공간이나 공집합이 아니다.)
$E_{1}$이 발생했다는 가정하에서 $E_{2}$가 일어날 조건부 확률은 $ \frac{P(E_{1} \cap E_{2})}{P(E_{1})} \equiv P(E_{2} \mid E_{1}) $ 이다.

 

읽을 때는 P $E_{2}$ bar $E_{1}$ 이라고 읽습니다.

 

위의 정의에 대해 좀 더 상세히 설명해보겠습니다. 먼저, 조건부 확률도 하나의 사건에 대한 확률이라는 것입니다. 그렇다면 $E_{1}, E_{2}$ 중 어느 사건에 대한 확률일까요?? 바로 $E_{2}$에 대한 확률입니다. 다만, $E_{1}$이 일어났다는 가정이 있어야합니다.

 

그런데 공식을 살펴보면 우리가 $E_{1}$에 대한 확률과 $E_{1} \cup E_{2}$에 대한 확률을 안다면 $E_{1}$과 $E_{2}$의 intersection($\cap$)을 구할 수 있지 않을까요? 이것이 곱셈 법칙입니다.

 

 

곱셈 법칙

 

$P(E_{1})$과 $P(E_{2} \mid E_{1})$이 주어질 때 $P(E_{1} \cap E_{2}) = P(E_{1}) \cdot P(E_{2} \mid E_{1})$ 이 성립한다.

 

간단한 예제를 통해서 한 번 살펴봅시다. 오늘의 주인공은 테스형으로 해보겠습니다.

 

$E_{1}$: 테스형이 미생물학 수업을 신청하는 사건
$E_{2}$: 테스형이 A학점을 받을 사건 이라면

$(E_{2} \mid E_{1})$은 테스형이 미생물학 수업에서 A학점을 받을 사건이겠죠?

 

우리가 P($E_{1}$) = $\frac{1}{2}$ 와 P($ E_{2} \mid E_{1}$) = $\frac{2}{3}$인 것을 알고 있다고 해봅시다. 우리가 알고 싶은 것은 테스형이 미생물학 수업을 신청하여서 A학점을 받는 사건의 확률(즉, P($E_{1} \cap E_{2}$)를 알고 싶습니다.

 

위의 곱셈 법칙을 통하여 우리는 이 사건의 확률이 $P(E_{1} \cap E_{2}) = P(E_{1}) \cdot P(E_{2} \mid E_{1}) = \frac{1}{2} \cdot \frac{2}{3} = \frac{1}{3}$임을 알 수 있습니다.

 

 

여기서, 테스형이 미생물학 수업에서 A학점을 받을 사건과 테스형이 미생물학 수업을 신청하여서 A학점을 받는 사건은다르다는 것이 헷갈리실 수 있습니다.

 

테스형이 미생물학 수업에서 A학점을 받을 사건은 테스형이 미생물학 수업을 신청할 지 안할지 모르지만 그 수업에서 A학점을 받을 사건을 말하는 것입니다.

하지만, 테스형이 미생물학 수업을 신청하여서 A학점을 받는 사건은 테스형이 꼭 미생물학 수업을 신청해야 하고, 그 수업에서 A학점을 받는 사건을 말하는 것입니다.

 

 

 

베이즈 정리에 관하여 알아보기 전에 알아야 할 개념이 있습니다. 바로 분할과 전확률공식입니다.

 

 

분할

 

사건들 $E_{1}, E_{2}, ... , E_{n}$이 $\bigcup_{i=1}^{n}E_{i} = S$ 이고, $ E_{i} \cap E_{j} = \phi $ 일 때, $E_{1}, E_{2}, ... , E_{n}$을 S의 분할이라 한다.

 

직관적으로 나타내기 위해 다음과 같은 그림을 그려보았습니다. (분할은 검은색 그림만 보시면 될 것 같습니다.)

 

 

 

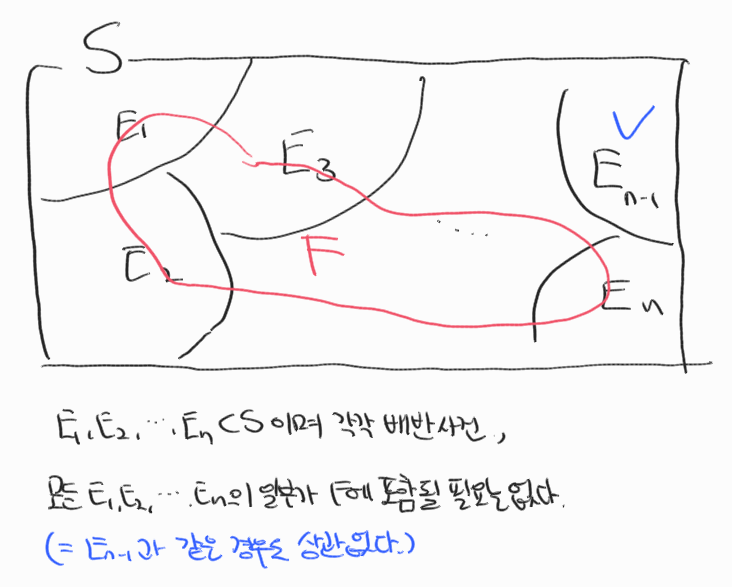
분할에 대해서 알아보았다면 이제 전확률 공식에 대해서 알아봅시다.

 

전확률공식

S가 하나의 표본공간이고 사건들 $E_{1}, E_{2}, ... , E_{n}$이 S의 분할이라 하자. 또한, $1 \leq i \leq n $, P($E_{i}$)는 주어지고 하나의 사건 $F_{1}$에 대해서 $P(F \mid E_{i})$ 가 주어졌다고 하자.
이때, $P(F) = \sum_{i=1}^{n}P(E_{i}) \cdot P(F \mid E_{i})$ 을 만족한다.

 

이는 조건부확률의 곱셈 법칙을 잘 활용한 것입니다. 이렇게 식으로만 봐서는 와닿지 않을 것 같네요. 쉽게 하나 예를 들면서 생각해봅시다.

 

우리나라의 전국 투표율$P(F)$을 알고 싶습니다. 우리가 알고 있는 것은 각 도의 인구 비율 $E_{1}, E_{2}, ... , E_{n}$과 각 도의 투표율$P(F \mid E_{i})$ 뿐 입니다. 우리는 전확률 공식에 의하여 각 도의 인구비율과 투표율을 곱하여 전국 투표율을 얻을 수 있는 것$P(F) = \sum_{i=1}^{n}P(E_{i}) \cdot P(F \mid E_{i})$입니다.

 

 

전확률 공식의 증명은 다음과 같습니다.

 

$ P(F) = P(F \cap S) = P(F \cap \bigcup_{i=1}^{n} E_{i}) $ $E_{1}, E_{2}, ... , E_{n}$은 S의 분할이므로
$ = P[(E_{1} \cap F) \cup (E_{2} \cap F) \cup ... \cup (E_{n} \cap F) ] $
$ = P(E_{1} \cap F) + ... + P(E_{n} \cap F) $ 확률의 공리에 의하여
$ = P(E_{1}) \cdot P(F \mid E_{1}) + ... + P(E_{n}) \cdot P(F \mid E_{n}) $
$ = \sum_{i=1}^{n}P(E_{i}) \cdot P(F \mid E_{i}) $

 

 

이제 드디어 베이즈 정리에 대해 알아봅시다. 베이즈 정리에서도 전확률공식에서 했던 가정을 그대로 하고, 전확률공식을 이용합니다.

 

 

베이즈 정리

 

S가 하나의 표본공간이고 사건들 $E_{1}, E_{2}, ... , E_{n}$이 S의 분할이라 하자. 또한, $1 \leq i \leq n $, P($E_{i}$)는 주어지고 하나의 사건 $F_{1}$에 대해서 $P(F \mid E_{i})$ 가 주어졌다고 하자.
이때, $P(E_{i} \mid F) = \frac{P(E_{i} \cap F)}{P(E)} =P(E_{i}) \cdot P(F \mid E_{i})$이다.

아까 들었던 예를 생각하며 이번 베이즈 정리의 의미를 곱씹어 봅시다. 우리는 이제 투표한 사람 중에서 한 사람을 뽑았을 때 그 사람이 특정 도의 사람일 확률$P(E_{i} \mid F)$이 궁금해졌습니다. 우리는 이를 특정 도의 인구비율(특정 도의 사람인 사건의 확률)$P(E_{i})$과 특정 도에서의 투표율(특정 도 사람이 투표하는 사건의 확률)$P(F \mid E_{i})$의 곱을 통해 알 수 있는 것입니다.

 

 

처음에 동시에 일어나는 사건이 아닌 사건에 대해서 알아본다고 하였죠? 이것에 초점을 두고 다시 한 번 살펴볼까요?

$P(E_{i} \mid F)$ 는 먼저 일어나는 사건은 F(투표한 사람을 고르는 사건)입니다. 그 후 사건 E(특정 도 사람인 사건)이 일어날 확률을 우리는 궁금해 한 것이지요.

 

 

그런데 우리는 이 사건이 일어난 시간 순서의 반대인 사건의 확률을 통해 구할 수 있다는 것입니다. 이게 무슨 말이죠?

아까, $P(E_{i})$(특정 도 사람인 사건)과 $P(F \mid E_{i})$(특정 도 사람이 투표하는 사건), 두 사건의 확률의 곱을 통해 구할 수 있다고 했지요?

 

$P(F \mid E_{i})$특정 도 사람이 투표하는 사건에서 먼저 일어나는 사건은 특정 도 사람인 사건이고 그 후에 일어나는 사건이 투표를 하는 사건입니다. 우리가 구하고 싶은 사건이 일어난 시간 흐름과는 반대인 사건을 우리는 베이즈 정리를 통해 구할 수 있는 것입니다!

 

 

오늘은 적다보니 많은 양을 적게 되었네요. 다음 주에는 독립사건에 대해 알아보도록 하겠습니다.

 

 

2021.01.29

 

- 히비스서커스 -