[기초확률론 6] 확률변수와 확률분포함수

기초확률론 여섯번째 포스팅으로 확률변수와 확률분포함수에 대해 알아보겠습니다.

 

 

저번 시간에는독립사건에 대해 알아보았습니다.

2021.02.05 - [Statistics/Probability_Theory] - [기초확률론 5] 독립사건

[기초확률론 5] 독립사건

 

이번에 살펴볼 확률변수 개념은 저의 개인적인 생각으로 확률론의 핵심이라고 생각합니다. 또한, 수리통계학을 공부하는데에 있어서 모르면 안될 너무나 중요한 개념이기도 하죠. 아무리 강조해도 중요한 개념이기에 꼭 살펴보시길 바라겠습니다.

 

 

확률변수의 정의에 대해 바로 알아보기에 전에 앞의 내용들을 정리해보며 확률변수가 왜 필요한지를 전체적으로 정리해보겠습니다.

 

 

우리는 지금까지 확률실험 하에서 표본공간을 구하고 확률측도를 통해 확률을 구하였었죠.

확률실험이란, 실험에 모든 결과를 알 수 있으나 실제 실험을 하기 전에는 결과를 알 수 없고 동일한 조건에서 반복할 수 있는 실험입니다.
표본공간이란, 확률실험이 일어났을 때 나올 수 있는 결과들의 집합입니다.

 

 

표본공간에는 이산표본공간과 연속표본공간이 존재하였습니다.

이산표본공간이란 표본공간의 수가 유한개인 경우를 말합니다.
연속표본공간이란 표본공간의 수가 무한개인 경우를 말합니다.

 

 

두 표본공간의 확률측도는 달랐습니다.

이산표본공간의 확률측도는 시그마를 통해 확률을 구하였습니다.
연속표본공간의 확률측도는 적분을 통해 확률을 구하였습니다.

 

 

 

 

이산표본공간에서 예를 들어 설명해보겠습니다. (H: Head로 동전의 앞면, T: Tail로 동전의 뒷면)

확률실험: 동전을 세 번 던지는 실험
표본공간: $S$ = {$HHH, HHT, HTH, THH, TTH, THT, HTT, TTT$}, (H: Head로 동전의 앞면, T: Tail로 동전의 뒷면)
확률: 임의의 $\omega \in S$, P({$\omega$}) = $\frac{1}{8}$

 

 

여기서, 저희가 동전의 앞면이 0, 1, 2, 3번 나오는 사건에 대해서 확률을 구하고 싶다고 해봅시다. 이를 나타내보면 다음과 같습니다.
$E_{0}$ = {$TTT$}, $P(E_{0}) = \frac{1}{8}$
$E_{1}$ = {$TTH, THT, HTT$}, $P(E_{1}) = \frac{3}{8}$
$E_{2}$ = {$HHT, HTH, THH$}, $P(E_{2}) = \frac{3}{8}$
$E_{3}$ = {$HHH$}, $P(E_{3}) = \frac{1}{8}$

 

 

이를 좀 더 간단하게 나타내는 방법을 한 번 생각본다면 함수를 사용하는 방법이 있을 겁니다. 함수 X를 동전을 세 번 던졌을 때 나오는 H의 수라 해봅시다.

 

 

$X(TTT) = 0$, $P(X=0) = \frac{1}{8}$
$X(TTH) = X(TTH) = X(TTH) = 1$, $P(X=1) = \frac{3}{8}$
$X(HHT) = X(HTH) = X(THH) = 2$, $P(X=2) = \frac{3}{8}$
$X(HHH) = 3$, $P(X=3) = \frac{1}{8}$

 

 

확률변수를 사용하니 확률변수에 따라서 확률의 분포를 확인하기 용이할 것 같지 않나요? 확률변수에서 중요한 점은 확률변수는 분포를 갖는다는 점입니다.

 

 

 

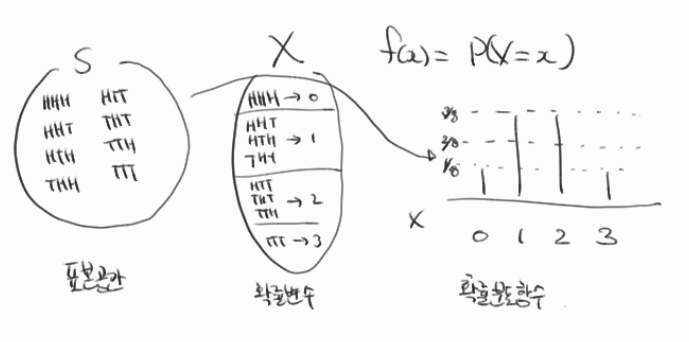
확률변수

이제 확률변수(random variable) 개념에 대해서 알아봅시다.

정의

확률변수란, 정의역이 표본공간이고 공역이 실수인 함수이다.

분류

1) 이산형 확률변수: 확률변수 $X$가 가질 수 있는 값이 셀 수 있을 때, (셀 수 없을 때도 가능)
2) 연속형 확률변수: 확률변수 $X$가 가질 수 있는 값이 셀 수 없을 때

기호정의

P({$\omega \in S | X(\omega) \in B$ }) $\equiv P(X \in B)$, $B \subset \mathbb{R}$

 

 

 

다음으로 확률측도에 확률변수를 넣어준 함수인 확률분포함수에 대해서 알아보도록 하죠. 앞서 확률변수는 분포를 갖는다고 하였죠? 확률분포는 확률변수가 취하는 값에 대한 가능성을 확률적 구조로 나타낸 것이라고 할 수 있습니다. 확률변수가 이산형 확률변수인 경우와 연속형 확률변수인 경우가 있으므로 이때의 확률분포함수도 다르겠죠? 한 번 살펴보도록 합시다. (참고 . 여기서는 연속표본공간에 대해 이산형 확률변수를 갖는 경우는 생각하지 않았습니다.)

 

 

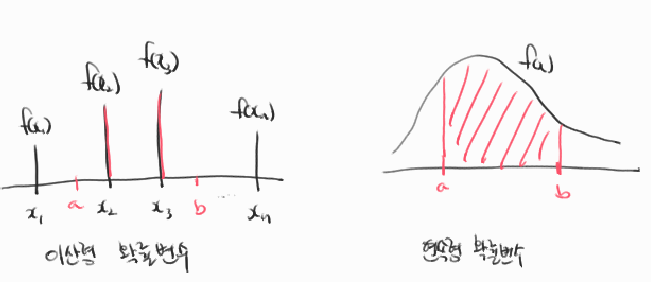
확률분포함수

임의의 $x \in \mathbb{R}$에 대해서 확률변수$X$의 확률분포함수가 $f(x)$이다 <=> $X$ ~ $f(x) = P(X = x)$

1) 이산형 확률변수인 경우

• $0 \leq f(x) \leq 1$
• $\sum_{x \in \mathbb{R}}^{} = 1$
• $P(a \leq X \leq b) = \sum_{a \leq X \leq b}^{} f(x)$

2) 연속형 확률변수인 경우

• $0 \leq f(x) \leq \infty$
• $\int_{-\infty}^{\infty} f(x) dx = 1$
• $P(a \leq X \leq b) = \int_{a}^{b} f(x) dx$

 

다음 시간에는 기댓값과 분산에 대해 알아보도록 하겠습니다.

 

 

 

 

 

2021.02.12

 

히비스서커스