| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- WSSS
- 히비스서커스
- GIT
- 백신후원
- 도커
- 티스토리챌린지
- Decision Boundary
- 기초확률론
- docker attach
- docker exec
- IVI
- 오블완
- numpy
- cs231n
- ssh
- aiffel exploration
- Jupyter notebook
- CellPin
- 사회조사분석사2급
- logistic regression
- cocre
- airflow
- Multi-Resolution Networks for Semantic Segmentation in Whole Slide Images
- docker
- vscode
- 프로그래머스
- HookNet
- AIFFEL
- 코크리
- Pull Request
- Today
- Total
히비스서커스의 블로그
[Column] 중심극한정리(CLT; central limit theorem) 본문
오늘은 통계학의 가장 중요한 개념이라고 할 수 있는 중심극한정리에 대해서 알아보도록 하겠습니다. 단순히 '많이 뽑으면 정규분포를 따르는 것 아니야?' 라고 생각하실 수 있지만,심층적 의미를 알아보려면 좀 더 디테일하게 살펴볼 필요가 있습니다. 이번 포스팅을 통하여 어디서 무엇을 많이 뽑는 것이고 어떤 것이 어떠한 형태의 정규분포를 따르게 되는 것인지 명확하게 알게 되셨으면 좋겠습니다.
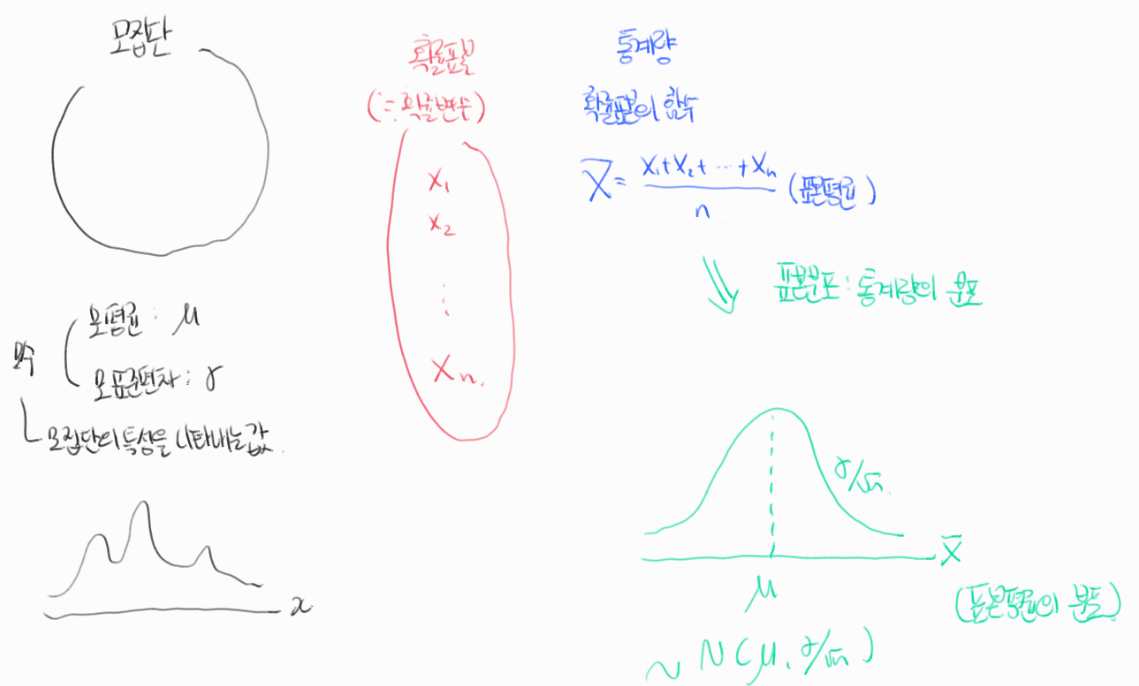
모집단과 표본집단
먼저 모집단과 표본집단에 대해서 알아볼 필요가 있습니다. 모집단이란 우리가 관심있는 대상 전체를 말합니다. 표본집단이란 모집단으로부터 추출된 모집단의 부분 집합이라고 할 수 있습니다.
예를 들어 생각해볼까요? 우리가 대전사람들의 평균 키를 구하고 싶다고 해봅시다. 여기서 모집단은 대전에 주민등록이 되어있는 모든 사람들입니다. 하지만 대전 지역에 거주하는 모든 사람들의 평균 키를 구할 수 없기 때문에 그 중의 일부를 뽑아서 구해야겠죠? 주민등록 상 대전이 거주지로 되어있는 사람들의 리스트를 모아서 일부를 추출한 집단이 표본집단입니다.
여기서 표본집단의 평균키가 모집단의 평균키와 동일할까요? 표본집단의 평균키가 모집단의 평균키라고 추정할 수는 있겠지만 모집단의 평균키라고는 할 수 없습니다. (뒤에 나오겠지만 표본평균이 모집단의 평균키라고 추정할 수 있는 근거가 중심극한정리에 담겨 있습니다.) 중심극한정리가 표본집단의 평균이 표본집단의 크기가 커지면 모집단의 평균과 같아진다고 생각한다면 큰일납니다.
확률표본
이제 표본집단이란 용어를 말고 확률표본이란 단어를 사용해보겠습니다. 확률표본이란 모집단에 속한 표본 하나하나가 표본으로 추출될 확률이 동일하다는 조건 하에서 추출된 표본입니다. 여기서 유의해야할 부분은 확률표본은 구체적인 관측치가 아닌 확률변수(정의역이 표본공간이고 치역이 실수인 함수)이기 때문에 표본에 속할 하나하나가 무엇일지는 사건이 일어나기 전까지 미리 알 수 없다는 것입니다.
여기서 우리가 관심있는 것은 확률표본의 수(크기)입니다. 확률표본을 여러 개(n개) 뽑아서 우리는 $X_{1}, X_{2}, ... , X_{n}$과 같이 나타낼 수 있습니다.
통계량과 표본분포
이번 내용을 이해하기 쉽게하기 위해 마지막으로 통계량과 표본분포의 개념을 알아보겠습니다.
통계량이란 쉽게 말하면 확률표본의 함수이고 대표적인 예로 확률표본의 표본평균, 표본분산 등이 있습니다.
표본분포란 통계량의 확률분포를 말합니다. 확률표본의 표본평균과 표본분산은 각각 어떤 분포를 따를 것입니다.
중심극한정리
드디어 오늘의 주인공인 중심극한정리에 대해 알아보도록 하겠습니다. 중심극한정리는 표본평균의 표본분포에 관한 것으로 이해하면 좋습니다. 모집단은 어떤 분포를 따를텐데(이항분포, 초기하분포, 균일분포, 정규분포 등등) 어떤 분포를 따르던지 상관없습니다. 이때 모집단은 평균이 $\mu$이고 표준편차가 $\sigma$입니다. 이때, 모집단에서 확률표본을 n개 만큼 뽑는다고 해봅시다. 그렇다면 확률표본의 표본평균은 통계량이므로 분포를 따를것입니다. 이 표본평균의 표본분포는 n이 커지면(일반적으로 $n \geq 30$) 평균이 $\mu$이고 표준편차가 $\frac{\sigma}{n}$인 정규분포를 따른다는 것입니다.
중심극한정리
모집단이 '평균이 $\mu$이고 표준편차가 $\sigma$인 임의의 분포'를 따른다고 할 때, 모집단으로부터 추출된 '표본의 크기(표본의 수)가 충분히 크다(일반적으로 $n \geq 30$)'면 표본 평균들이 이루는 분포는 '평균이 $\mu$이고 표준편차가 $\frac{\sigma}{\sqrt(n)}$인 정규분포'에 근사한다.
중심극한정리에 의의
그렇다면 중심극한정리가 왜 중요할까요?
통계학에서 중요한 부분 중 하나가 모집단의 특성(모수)를 추정하는 것입니다. 왜냐하면 모집단 전체를 조사하여 모집단의 특성을 알아내는 것은 거의 불가능에 가깝고, 시간과 비용이 많이 들기 때문이지요. 그래서 통계학의 여러 기법을 통해 모집단의 표본들을 통해서 모집단의 특성을 추정하는 것입니다.
각각의 표본은 모집단의 특성을 나타내기에는 부족할 것입니다. 하지만 (표본들의 더하여 그 개수만큼 나눈) 표본평균의 분포가 n이 커지기만 한다면 모집단의 특성을 나타낼 수 있게되는 것이죠. 즉, 통계량인 표본평균을 통해서 모집단의 모수(모집단의 특성을 나타내는 값)인 모평균과 모표준편차를 추정할 수 있는 확률적 근거를 제시해주는 것입니다. 더군다나 정규분포는 표준화하여 표준정규분포로 나타낼 수 있기 때문에 표준정규분포표 하나가 주어지면 확률값을 구하기도 쉽습니다.
정리하자면, 중심극한정리는 모집단의 모수를 추정하는데 큰 기여를 하고 있습니다.
- 히비스서커스 -
'Theory > Statistics' 카테고리의 다른 글
| [기초확률론 7] 기댓값과 분산 (0) | 2021.03.19 |
|---|---|
| [기초확률론 6] 확률변수와 확률분포함수 (2) | 2021.02.12 |
| [기초확률론 5] 독립사건 (0) | 2021.02.05 |
| [기초확률론 4] 조건부확률, 곱셈법칙, 베이즈 정리 (0) | 2021.01.29 |
| [기초확률론 3] 확률측도의 성질, 균등확률결과를 갖는 표본공간 (0) | 2021.01.22 |




